Che siate data scientist esperti o che abbiate iniziato da poco il vostro percorso di analisi, credetemi, a un certo punto della vostra carriera vi sarete imbattuti o vi imbatterete in almeno un progetto che prevede l’analisi di segmentazione/cluster. Si tratta probabilmente di una delle competenze di machine learning più diffuse e importanti che dovreste imparare e comprendere come data scientist.
In questo tutorial, vi guideremo attraverso un’analisi dei cluster su alcuni aspetti del mercato immobiliare della Carolina del Nord a partire da metà 2021. Identificheremo i cluster di questi quartieri in base alle loro somiglianze e differenze su alcune metriche chiave, utilizzando modelli ML non supervisionati. I dati grezzi provengono dal Redfin Data Center e possono essere scaricati gratuitamente.
In questo progetto pratico, analizzerete i dati del mercato immobiliare raccolti in 162 quartieri della Carolina del Nord e identificherete i cluster di questi quartieri in base alle loro somiglianze e differenze su alcune metriche chiave, utilizzando modelli ML non supervisionati. I dati grezzi provengono dal Redfin Data Center e possono essere scaricati gratuitamente.
Introduzione all’analisi dei cluster
Prima di lanciarci nella scrittura del codice, introduciamo alcuni concetti base sull’analisi dei cluster. L’analisi dei cluster è una tecnica di apprendimento automatico molto popolare, ampiamente utilizzata in molte applicazioni come la segmentazione dei clienti, l’elaborazione delle immagini e i sistemi di raccomandazione, solo per citarne alcune.
In generale, l’analisi dei cluster rientra nell’ambito dei modelli di apprendimento automatico non supervisionati. Un modello di Machine learning non supervisionato, come suggerisce il nome, non è supervisionato, ossia non vengono fornite all’algoritmo etichette preassegnate (ad esempio, etichette di cluster) per i dati di addestramento. Pertanto, il modello generato troverà, mediante un’analisi esplorativa, pattern nascosti ed estrarrà intuizioni dai dati stessi.
Esistono diversi tipi di algoritmi di clustering, come quelli basati sulla connettività, sui centroidi, sulla densità, sulla distribuzione e così via, ognuno dei quali presenta vantaggi e svantaggi ed è adatto a scopi e casi d’uso diversi. Alcuni di questi li abbiamo già descritti negli articoli DBSCAN: come funziona, K-Means: come funziona e Clustering gerarchico: come funziona.
In questo progetto, ci concentriamo principalmente sull’utilizzo di due delle tecniche di clustering sopra menzionate: il clustering gerarchico (basato sulla connettività) e k-means (basato sul centroide). Queste due tecniche di Machine Learning non supervisionate si basano entrambe sulla prossimità (utilizzando misure di distanza). Sono semplici ma molto efficaci e potenti in molti lavori di clustering.
Scaricare, leggere e preparare i dati
Per prima cosa, colleghiamo a Redfin, scorriamo fino alla sezione “Come funziona” e scarichiamo i dati della regione a livello di “quartieri”. Si tratta di un dataset (file .gz) che può essere scaricato e utilizzato gratuitamente.

Apriamo quindi il notebook Jupyter (vedere l’articolo Jupyter Notebook: guida al suo utilizzo), importiamo tutte le librerie necessarie e leggiamo i dati. Si tratta di un dataset piuttosto grande (circa 2 GB), quindi potrebbe essere necessario un pò di tempo per la lettura.
#Import all the necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler, normalize, RobustScaler, MinMaxScaler
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import scipy.cluster.hierarchy as hc
from sklearn.cluster import AgglomerativeClustering
#read in raw data (replace ... with your own file directory where the data was saved)
df_raw = pd.read_csv('./neighborhood_market_tracker.tsv000.gz', compression='gzip', sep='\t', quotechar='"')
Poiché il dataset è molto grande, per semplicità di analisi e di dimostrazione, ci concentriamo solo sulle proprietà “residenziali monofamiliari” vendute in NC da luglio 2021 fino ad oggi. Inoltre, filtriamo tutti i quartieri che hanno venduto meno di 20 proprietà in questo periodo.
#Filter the dataframe to only look at single-family properties sold in NC from 2021-07
df_NC=df_raw[(df_raw['period_begin'] =='2021-07-01') & (df_raw['property_type']=='Single Family Residential') & (df_raw['homes_sold']>=20) & (df_raw['state_code']=='NC')]
df_NC.head()
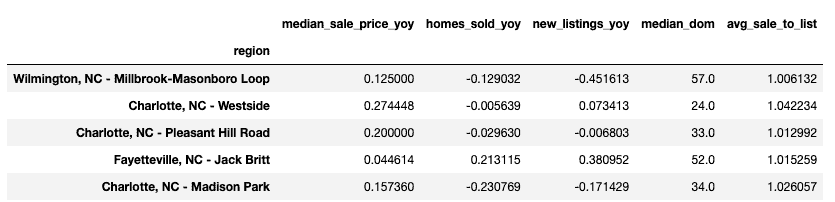
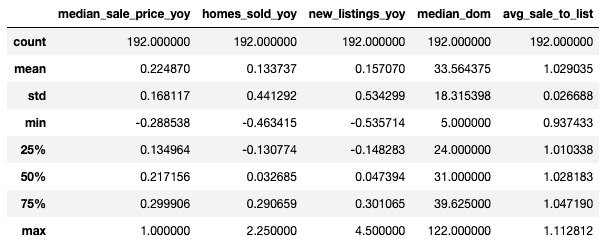
I dati grezzi si presentano come la tabella seguente, con un totale di 58 colonne. La colonna “region” è il nome del quartiere.

df_NC.info()

Per la nostra analisi di clustering, ci concentreremo solo su 5 caratteristiche. Pertanto, manteniamo solo i campi di interesse nel nostro frame di dati utilizzando il seguente codice.
#Select fields that are of interest
fields=[
'region',
'median_sale_price_yoy',
'homes_sold_yoy',
'new_listings_yoy',
'median_dom',
'avg_sale_to_list',
]
df=df_NC[fields].set_index('region')
df.head()
Pulizia dei dati
Verifichiamo rapidamente se ci sono valori mancanti o anomalie che devono essere trattate prima di procedere con l’analisi.
df.describe()
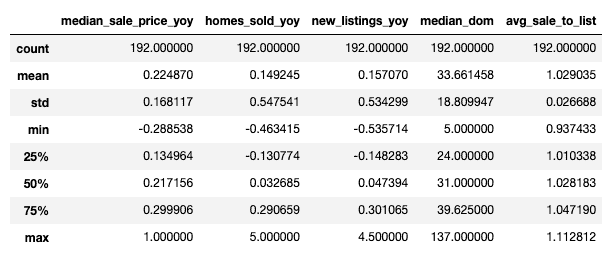
Dalle statistiche riportate sembra che i dati non presentino grandi anomalie. Non ci sono, infatti, valori mancanti per tutte le colonne. Diversamente, sembra che le caratteristiche “median_dom”, “median_sale_price_yoy” e “homes_sold_yoy” possano avere degli outlier potenzialmente grandi, mentre il resto delle caratteristiche sembra essere in un intervallo abbastanza ragionevole.
fig, ax = plt.subplots()
ax.boxplot(df['median_dom'])
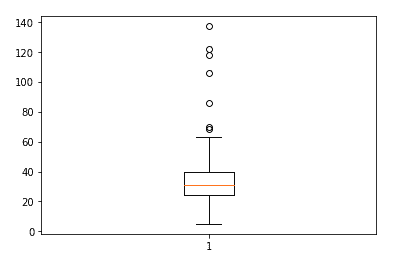
fig, ax = plt.subplots()
ax.boxplot(df[['median_sale_price_yoy', 'homes_sold_yoy', 'new_listings_yoy', 'avg_sale_to_list']])
plt.show()
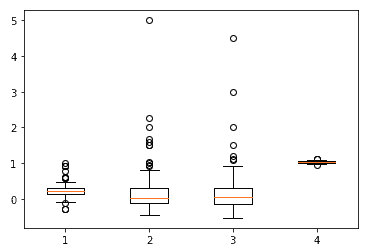
Trattiamo i valori anomali per “median_dom”, “median_sale_price_yoy” e “homes_sold_yoy” limitando il valore massimo al 99% del percentile utilizzando il codice seguente.
#Find the 99% percentile value in the 'median_dom' column
percentiles=df['median_dom'].quantile([0.00,0.99]).values
percentiles
#Replace the outlier with the 99% percentile value
df["median_dom"] = np.where(df["median_dom"] >=137, 53.039,df['median_dom'])
#Find the 99% value in the 'homes_sold_yoy' column
percentiles=df['homes_sold_yoy'].quantile([0.00,0.99]).values
percentiles
#Replace the outlier with the 99% percentile value
df["homes_sold_yoy"] = np.where(df["homes_sold_yoy"] >=5, 1.80475,df['homes_sold_yoy'])
#Find the 99% value in the 'median_sale_price_yoy'' column
percentiles=df['median_sale_price_yoy'].quantile([0.00,0.99]).values
percentiles
#Replace the outlier with the 99% percentile value
df["median_sale_price_yoy"] = np.where(df["median_sale_price_yoy"] >=1, 0.90592827,df['median_sale_price_yoy'])
df.describe()
Eseguire la PCA (Analisi delle componenti principali)
Prima di inserire le nostre caratteristiche in un algoritmo di clustering, consiglio sempre di eseguire prima la PCA sui dati. La PCA è una tecnica di riduzione della dimensionalità che consente di concentrarsi solo su alcune componenti principali in grado di rappresentare la maggior parte delle informazioni e della varianza dei dati.
Nel contesto dell’analisi dei cluster, in particolare in questo caso in cui non disponiamo di un gran numero di caratteristiche, il vantaggio principale dell’esecuzione della PCA è in realtà la visualizzazione. L’esecuzione della PCA ci aiuterà a identificare le 2 o 3 componenti principali principali in modo da poter visualizzare i nostri cluster in un grafico a 2 o 3 dimensioni.
Per eseguire la PCA, normalizziamo innanzitutto tutte le nostre caratteristiche alla stessa scala, poiché la PCA e i metodi di clustering basati sulla distanza sono sensibili agli outlier e alle diverse scale/unità.
#Scale all the features using min-max scaler
minmax_scaler=MinMaxScaler()
scaled_features=minmax_scaler.fit_transform(df)
Eseguiamo quindi l’analisi PCA e mostriamo le componenti principali che spiegano la maggior parte della varianza dei nostri dati utilizzando il codice seguente.
import matplotlib
%matplotlib inline
%config InlineBackend.figure_format='svg'
import matplotlib.pyplot as plt
plt.style.use('ggplot')
#Create a PCA instance
pca=PCA(n_components=5)
principalComponents=pca.fit_transform(scaled_features)
#Plot the expained variaces
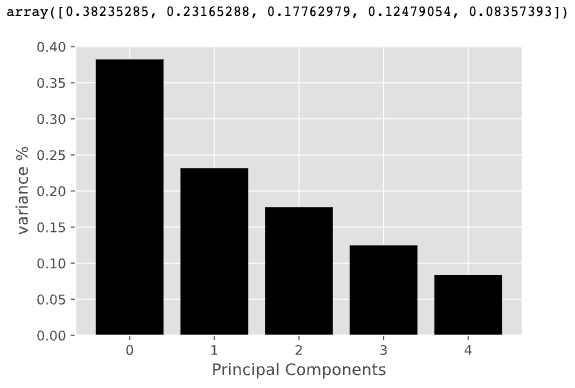
features=range(pca.n_components_)
plt.bar(features,pca.explained_variance_ratio_,color='black')
plt.xlabel("Principal Components")
plt.ylabel('variance %')
plt.xticks(features)
#Save components to a dataframe
PCA_components=pd.DataFrame(principalComponents)
#Show the expained variance by each principal component
pca.explained_variance_ratio_
Si può notare che le prime 3 componenti principali, combinate insieme, spiegano circa l’80% della varianza dei dati. Pertanto, invece di utilizzare tutte e 5 le caratteristiche per il nostro modello, possiamo utilizzare solo le prime 3 componenti principali per il clustering.
Infine, analizziamo i pesi di ciascuna variabile originale su queste componenti principali, in modo da avere una buona comprensione di quali variabili hanno maggiore influenza su quali componenti principali, o in altre parole, possiamo ricavare un significato per queste componenti principali.
weights=pca.components_
weights

Si tratta di un’analisi piuttosto interessante! Il PC1 è influenzato da ‘median_dom’ (giorni mediani di mercato), quindi questa componente principale rappresenta la velocità di vendita degli immobili in un quartiere. Possiamo etichettarla come “velocità di vendita”.
Il PC2 è largamente influenzato da ‘homes_sold_yoy’ (aumento del numero di case vendute rispetto allo stesso periodo dell’anno precedente), quindi rappresenta il volume delle vendite o la variazione delle nuove vendite rispetto all’anno precedente. Possiamo etichettarlo come “vendita/nuovi annunci”.
Il PC3 è largamente influenzato da “avg_sale_to_list” (rapporto tra il prezzo di vendita diviso per il prezzo di listino). Possiamo etichettare il PC3 come “variazione dei prezzi di vendita”.
Clustering gerarchico
Siamo pronti ad alimentare i nostri dati con un algoritmo di clustering! Per prima cosa proveremo il clustering gerarchico. La cosa più bella del clustering gerarchico è che permette di costruire un albero di cluster (chiamato “dendrogramma”) che visualizza le fasi del clustering. Poi si può tagliare l’albero orizzontalmente per selezionare il numero di cluster che hanno più senso in base alla struttura dell’albero.
#Create a dendrogram using hierarchical clustering
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(7, 5))
plt.title("Dendrogram")
dend = shc.dendrogram(shc.linkage(PCA_components, method='ward'))
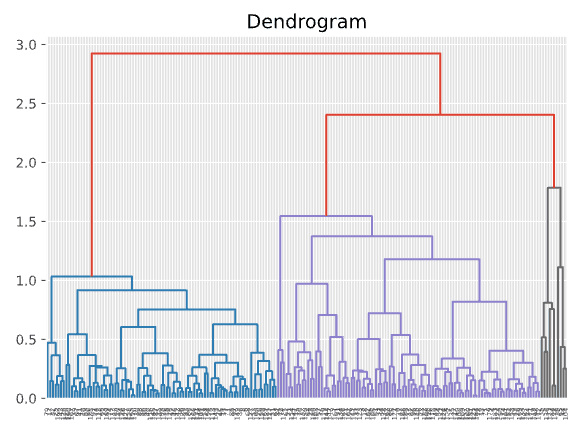
Nel dendrogramma qui sopra, possiamo vedere che a seconda di dove si posiziona la linea orizzontale si ottiene un numero diverso di cluster. Sembra che 4 cluster o 5 cluster siano entrambe soluzioni ragionevoli. Tracciamo la soluzione a 4 cluster in un grafico di dispersione e vediamo come appare.
#Plot scatter plot
agc = AgglomerativeClustering(n_clusters = 4)
plt.figure(figsize =(6, 4))
plt.scatter(PCA_components[0],PCA_components[1], c = agc.fit_predict(PCA_components), cmap ='rainbow')
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.title("Agglomerative Hierarchical Clusters - Scatter Plot", fontsize=18)
plt.show()
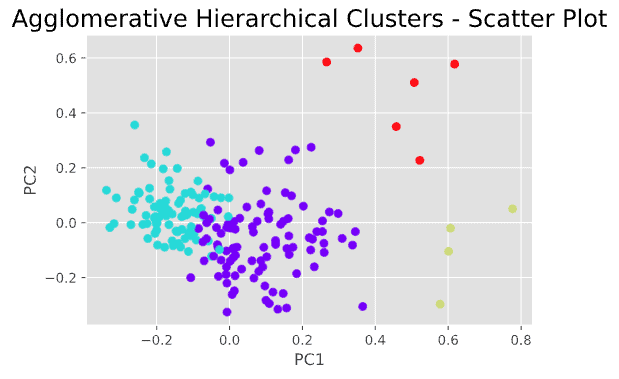
Questo non è male e ci dà una comprensione di base del numero di possibili cluster che possono esistere in questi dati e di come questi cluster appaiono in un grafico a dispersione. Tuttavia, i risultati della clusterizzazione gerarchica non sembrano ideali, in quanto si può notare che ci sono alcuni punti dati “discutibili” che potrebbero essere assegnati ai cluster sbagliati.
Il clustering gerarchico, sebbene sia molto utile per visualizzare il processo di clustering attraverso una struttura ad albero, presenta alcuni svantaggi. Ad esempio, il clustering gerarchico effettua un solo passaggio attraverso i dati. Ciò significa che i record allocati o assegnati in modo errato all’inizio del processo non possono essere riassegnati successivamente.
Pertanto, raramente interrompiamo la nostra analisi con la soluzione di clustering gerarchico, ma piuttosto la utilizziamo per ottenere una comprensione “visiva” di come potrebbero apparire i cluster, per poi utilizzare un metodo iterativo (ad esempio, k-means) per migliorare e perfezionare le soluzioni di clustering.
Utilizzo del K-means
K-means è un metodo di clustering molto popolare con il quale si specifica un numero desiderato di cluster, k, e si assegna ogni record a uno dei k cluster in modo da minimizzare una misura di dispersione all’interno dei cluster.
Si tratta di un processo iterativo che assegna e rialloca i punti di dati per minimizzare la distanza di ogni record dal centroide del suo cluster. Alla fine di ogni iterazione, si ottiene un certo miglioramento e la procedura viene ripetuta fino a quando il miglioramento è molto ridotto.
Per eseguire il clustering k-means, occorre innanzitutto specificare k (numero di cluster). Possiamo farlo in due modi:
- Specificare k utilizzando la nostra conoscenza del dominio o l’esperienza passata.
- Eseguire un clustering gerarchico per ottenere una prima comprensione del numero di cluster da provare.
- Utilizzare il metodo “Elbow” per determinare k
Dal dendrogramma del passo precedente, sappiamo già che k=4 (o k=5) sembra funzionare abbastanza bene. Possiamo anche usare il metodo del “gomito” per verificare di nuovo. Il codice sottostante traccia il grafico di “Elbow” che ci dice dove si trova il punto di svolta per il numero ottimale di cluster.
#Elbow method
ks=range(1,20)
inertias=[]
for k in ks:
model=KMeans(n_clusters=k)
model.fit(PCA_components.iloc[:,:3]) #we only use the first 3 principal components
inertias.append(model.inertia_)
plt.plot(ks,inertias, '-o',color='black')
plt.xlabel('number of clusters, k')
plt.ylabel('inertia')
plt.xticks(ks)
plt.show
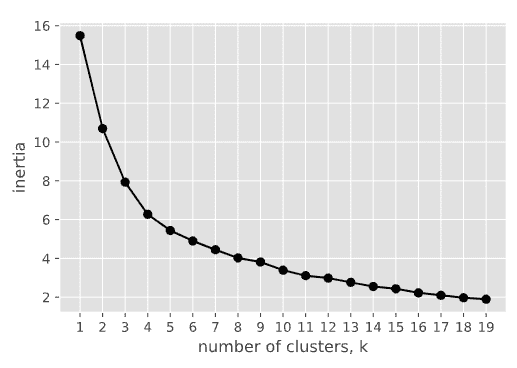
I risultati sono abbastanza coerenti con quelli ottenuti dal dendrogramma: sia 4 che 5 sono un numero ragionevole di cluster da provare, quindi proviamo k=5. Il codice seguente genera il diagramma di dispersione 3D per 5 cluster.
#plot 3-D scatter plot
from matplotlib import pyplot
from mpl_toolkits.mplot3d import Axes3D
kmeans=KMeans(n_clusters=5, init='k-means++',random_state=42)
kmeans.fit(PCA_components.iloc[:,:3])
labels=kmeans.predict(PCA_components.iloc[:,:3])
fig = pyplot.figure()
ax = Axes3D(fig)
ax.scatter(PCA_components[0],PCA_components[1],PCA_components[2],c=labels)
pyplot.show()
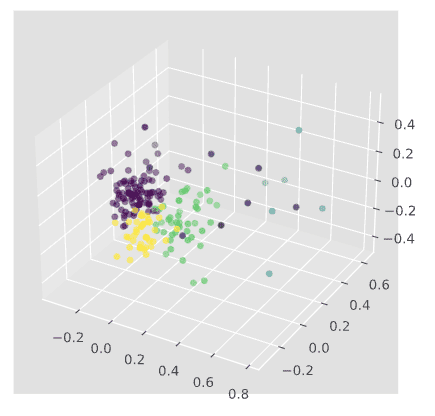
Descrivere i cluster e ricavare le informazioni principali
Ora che abbiamo i nostri cluster, aggiungiamo le etichette dei cluster al data frame originale (df_NC), esportiamolo in un file .csv e ricaviamone alcune osservazioni.
#Add cluster labels to the original dataset and export to csv file
df_NC['cluster_nbr']=kmeans.labels_
df_NC_clusters=pd.concat([df_NC.reset_index(drop=True),pd.DataFrame(principalComponents)],axis=1)
df_NC_clusters.to_csv('df_NC.csv')
Utilizzando poi strumenti di creazione di dashboard come Tableau o Google Looker, possiamo visualizzare i cluster in termini di caratteristiche, somiglianze e differenze.


