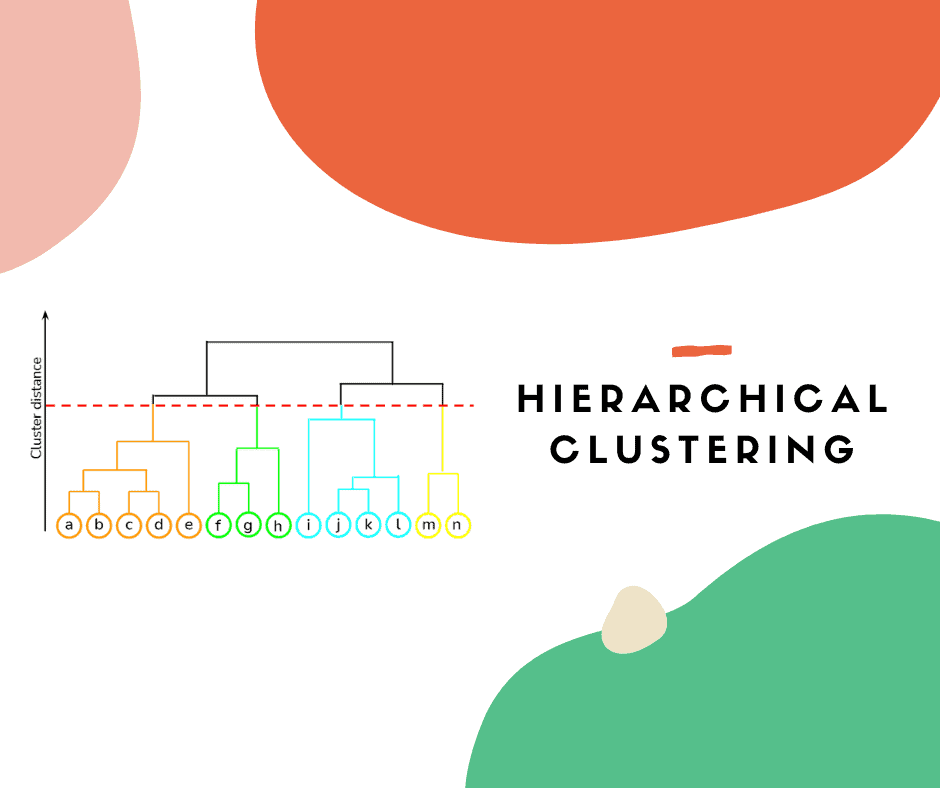
Gli algoritmi di clustering permettono di raggruppare dati non etichettati in gruppi che condividono delle caratteristiche. Esistono diversi metodi e alcuni di essi li abbiamo spiegati negli articoli DBSCAN: come funziona e K-Means: come funziona. In questo articolo tratteremo invece il clustering gerarchico. Questa metodologia permette di creare una gerarchia tra i punti di dato che può essere poi usata per definire i gruppi (ossia i cluster). Scopriamo come funziona passo dopo passo.
Supponiamo che un negozio abbia collezionato l’età di 9 clienti, etichettati come C1-C9, e l’importo speso da ciascuno di loro nel negozio nell’ultimo mese.
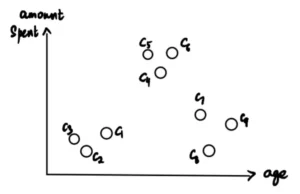
Ora il negozio vuole identificare i segmenti o i cluster dei suoi clienti per capire meglio le loro esigenze. Per far ciò, i data scientist (cioè noi), siamo incaricati di analizzare i dati. In questo contesto, avendo anche pochi dati, useremo il clustering gerarchico.
Creazione di cluster e dendrogrammi
Iniziamo facendo di ogni singolo punto di dati un cluster. Si formano così 9 cluster:
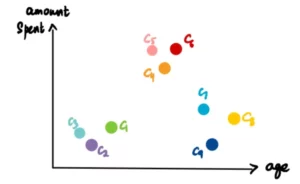
Prendiamo i due cluster più vicini (per misura la distanza vi rimandiamo alla sezione Distanze) e farne un unico cluster. Poiché C2 e C3 sono i più vicini, formano un cluster. In questo modo si ottiene un totale di 8 cluster.
Ora rappresentiamo questo cluster con un grafico chiamato Dendrogramma. L’asse delle ascisse rappresenta i punti (nel nostro caso i clienti) e l’asse delle ordinate la distanza tra i cluster.
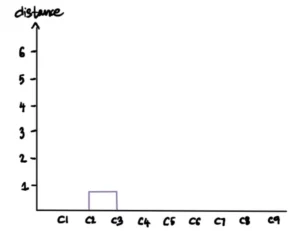
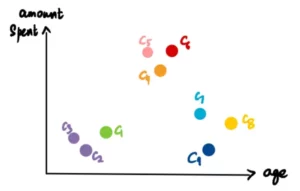
Ripetiamo l’operazione precedente. Prendiamo i due cluster più vicini (C5 e C6), li trasformiamo in un unico cluster e lo tracciamo sul dendrogramma.
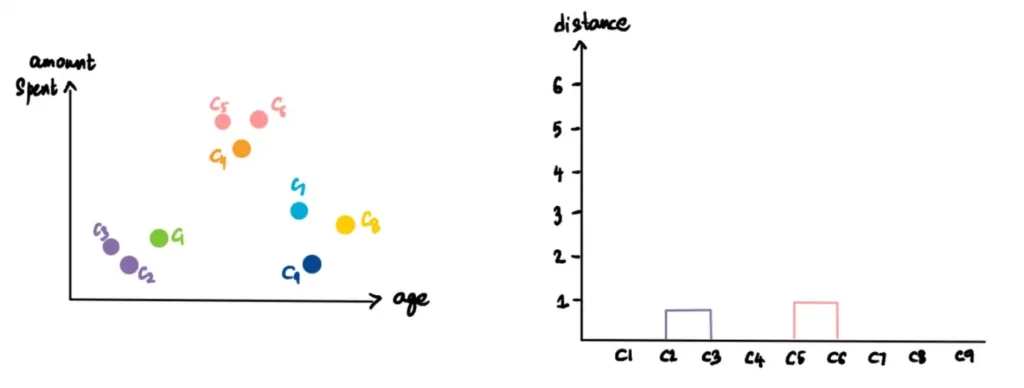
Continuiamo a ripetere questo processo finché non rimane un solo cluster.
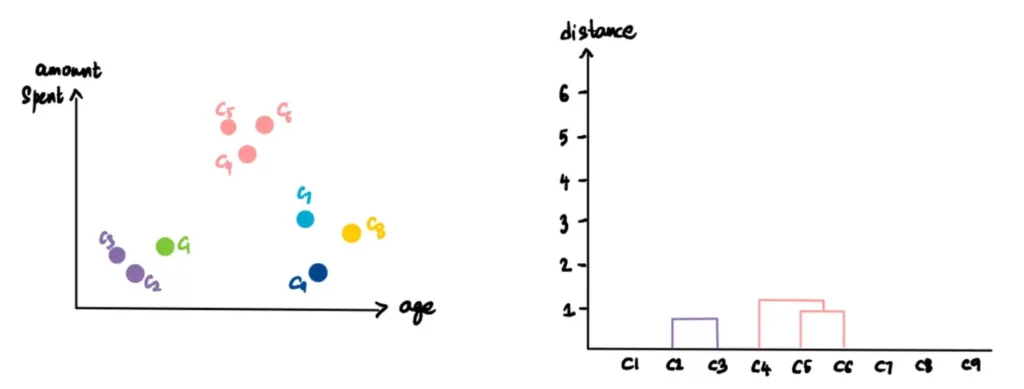
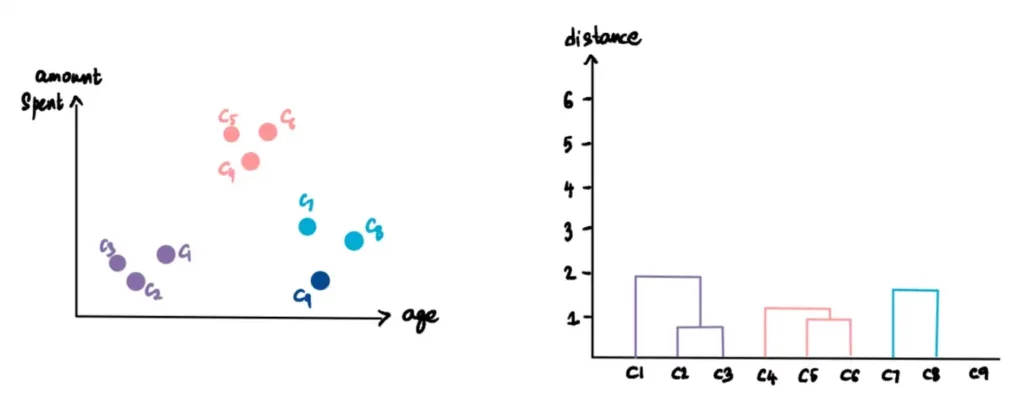
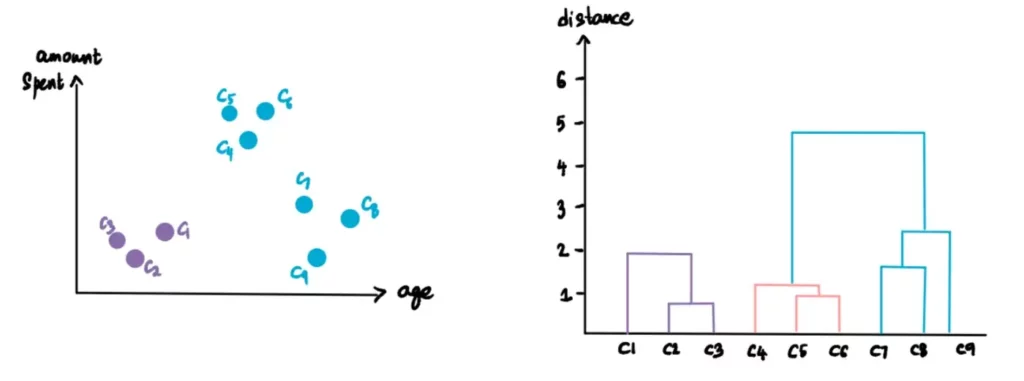
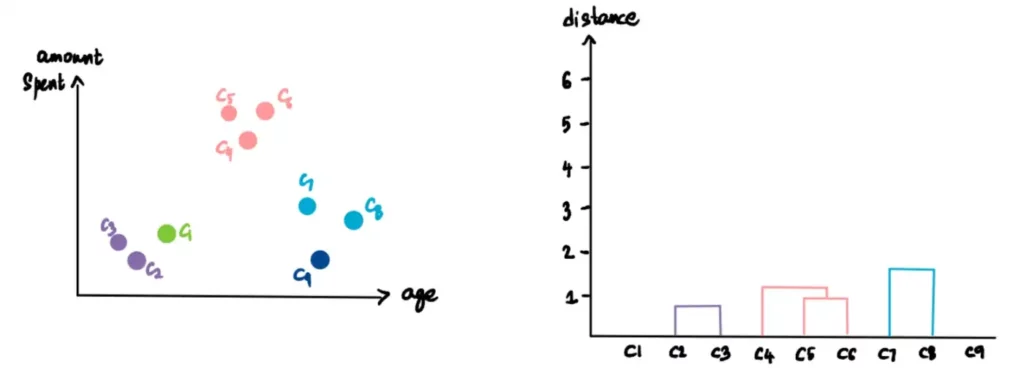
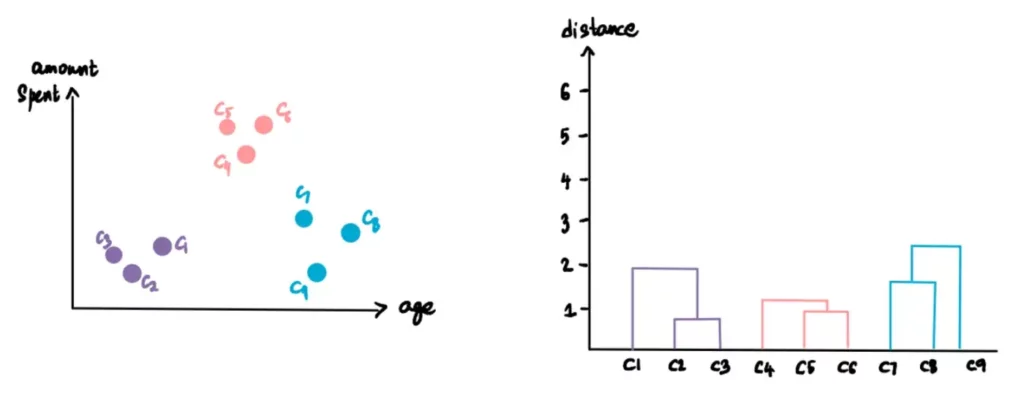
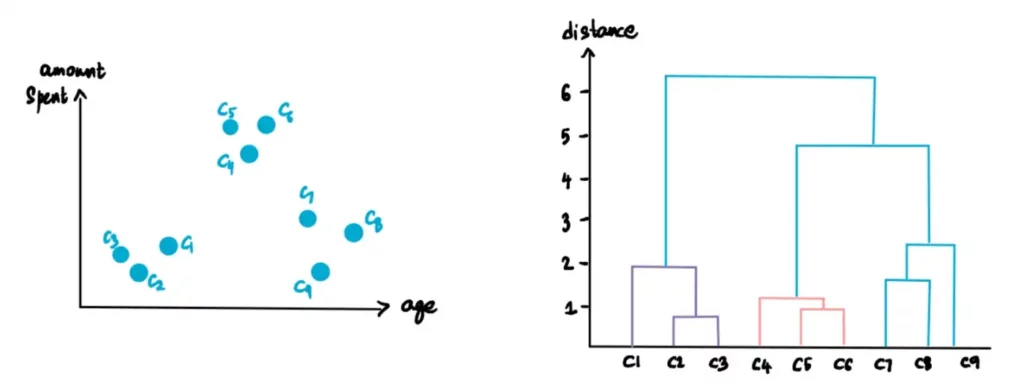
Ecco come creare il dendrogramma e i cluster gerarchici.
Distanze
In precedenza, abbiamo parlato di trovare i cluster più vicini, ma come misuriamo esattamente questa vicinanza?
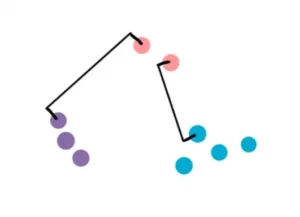
Immaginiamo di avere i cluster rosa, blu e viola. Ora vogliamo capire se dobbiamo raggruppare il cluster rosa con quello blu o con quello viola.

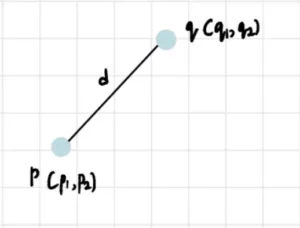
Esistono 4 modi per farlo. Ma prima di parlarne, parliamo brevemente della distanza. In questo contesto, quando parlo di distanza intendo la distanza euclidea. Quindi, se p con coordinate (p₁, p₂,…, pₙ) e q con coordinate (q₁, q₂,…, qₙ) sono due punti in n-dimensioni, la distanza euclidea tra loro è:
Nel nostro caso, poiché i dati sono bidimensionali, la distanza euclidea tra due punti sarà:
Ovviamente si possono usare altre distanze come già discusso nell’articolo del K-Means. Per darvi un’indicazione rapida, le distanze maggiormente usate, oltre a quella euclidea, sono quella di Manhattan, Minkowski e del coseno.
Ora che abbiamo capito come interpretare le distanze, i 4 modi per determinare la vicinanza sono:
Single-Linkage: nel metodo single-linkage, definiamo la distanza come la distanza più breve tra due punti in ciascun cluster. Pertanto, confrontiamo la distanza tra i punti più vicini nei cluster rosa e viola con la distanza tra i punti più vicini nei cluster blu e rosa. La più piccola delle due distanze determina il cluster più vicino a quello rosa.
Complete-Linkage: è simile al Single-Linkage, ma in questo caso la distanza viene misurata tra la coppia di punti più lontana di due cluster.

Average Linkage: come suggerisce il nome, la distanza è definita come la distanza media tra ogni punto del primo cluster e ogni punto del secondo cluster. La formula matematica per calcolare la distanza è la seguente:
Non spaventatevi! L’importante è che capiate l’idea che è alla base del metodo.
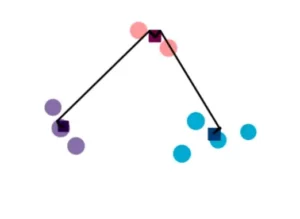
Metodo del centroide: si tratta di trovare il centroide di ciascun cluster e quindi di trovare la distanza tra di essi. Per il calcolo del centroide vi rimando all’articolo sul K-means.
Ulteriori informazioni sui cluster
Personalizzazione dei cluster
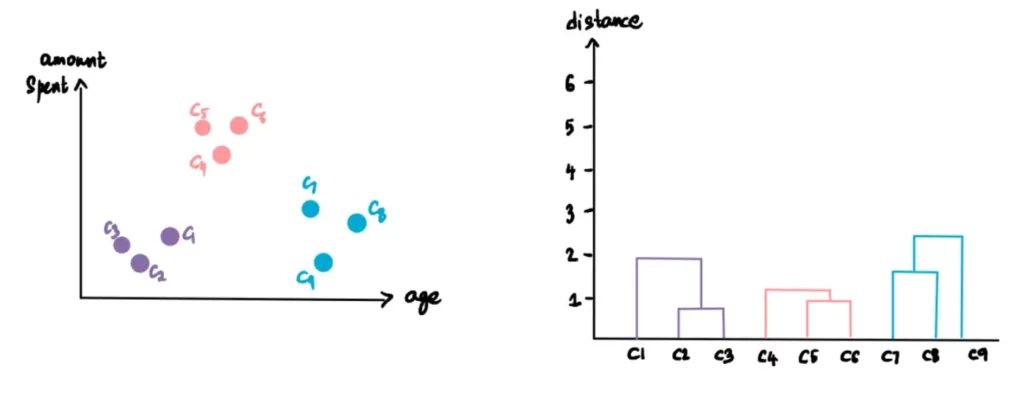
Sappiamo che il nostro dendrogramma finale ha questo aspetto:
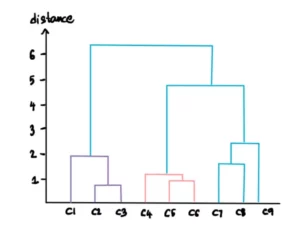
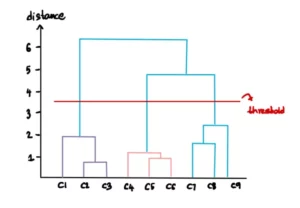
È possibile personalizzare il numero di cluster desiderati specificando una soglia per la distanza. Ad esempio, supponiamo che non vogliamo cluster con distanze superiori a 3. Allora tracciamo una linea per la soglia pari a 3:
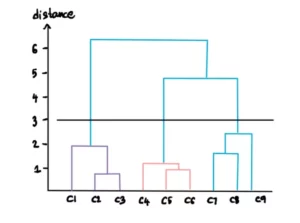
Questa linea implica che al di là di questo livello i cluster non saranno considerati. Pertanto, rimangono solo i 3 cluster al di sotto della linea di soglia:
Se impostiamo la soglia della distanza a 5
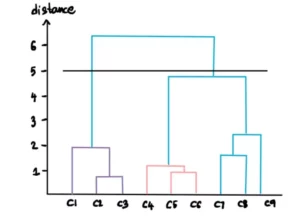
allora otterremo solo 2 clusters
Numero ottimale di cluster
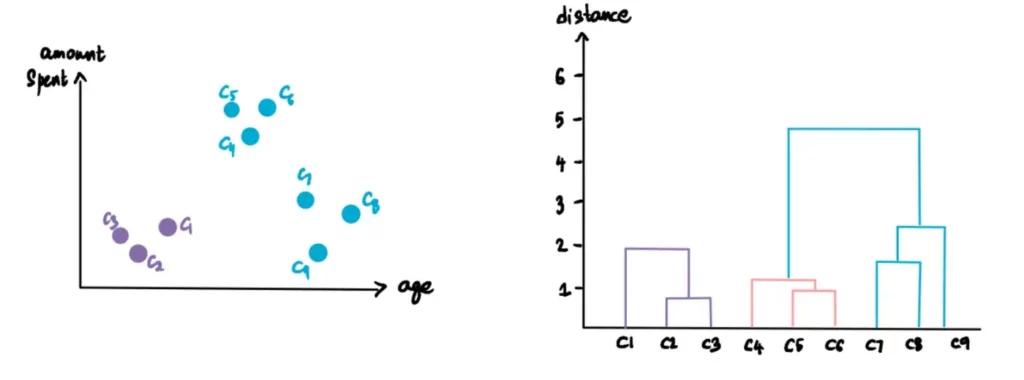
Il numero ottimale di cluster si ottiene trovando la linea più lunga che non attraversa nessuna linea orizzontale (soglia). Nel nostro caso, questa sarà la linea più lunga:
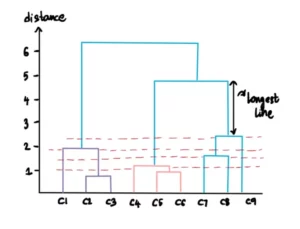
Dobbiamo quindi tracciare una linea orizzontale che attraversi questa linea di distanza massima e questa sarà la soglia per calcolare i cluster. Il risultato sarà il seguente:
Come utilizziamo i cluster ottenuti?
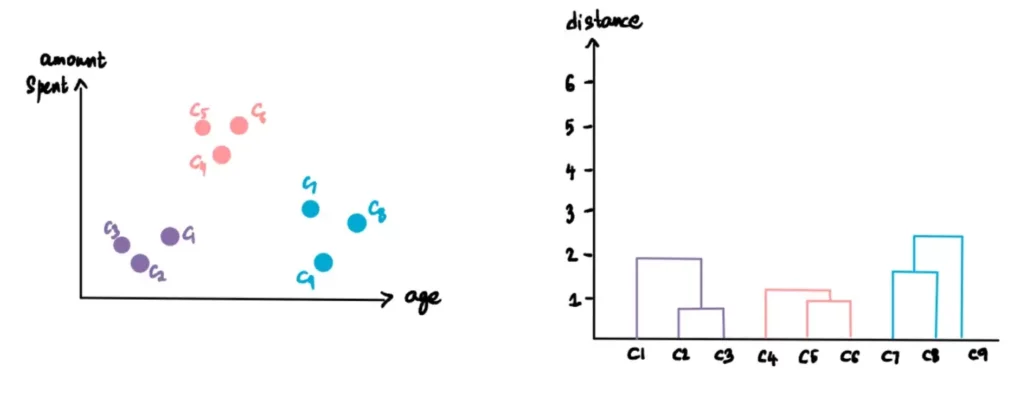
Ora che abbiamo terminato il processo di clusterizzazione e che abbiamo scoperto che ci sono 3 cluster ottimali, quali sono le deduzioni che il negozio può trarre da questo?
Nel nostro esempio, supponiamo che le caratteristiche comuni dei punti appartenenti a ciascun cluster determino 3 categorie: i clienti più giovani che non spendono molto, i clienti più anziani che spendono meno e il segmento medio che spende molto. Il negozio può ora utilizzare queste informazioni a suo vantaggio. Può ottimizzare la propria attività amplificando i servizi, i prodotti e le offerte offerti al terzo segmento di clienti di mezza età. Può riunire le proprie risorse per rendere questo gruppo più felice: offrire loro più scelte che soddisfino i loro gusti, portare i prodotti più recenti o persino offrire loro orari di shopping esclusivi.
Questo è un semplice esempio di come si può utilizzare il clustering, ma le possibilità sono infinite!