Nel campo del machine learning esistono diversi algoritmi per raggruppare i dati. Nell’articolo DBSCAN: come funziona abbiamo analizzato il DBSCAN che fornisce dei risultati molto robusti in caso di presenza di outliers e di forme non globulari. Nonostante ciò, in alcuni contesti applicativi non si può sempre applicare e/o i suoi risultati non sono ottimali. In questo articolo spiegheremo un altro algoritmo: il K-Means. È un algoritmo di clustering molto popolare. Senza entrare nei dettagli più tecnici e matematici dell’approccio, spiegheremo l’intuizione che c’è dietro.
Prima di iniziare con l’algoritmo, ripassiamo cos’è il clustering. Il clustering consiste nella scoperta automatica di raggruppamenti naturali nei dati. Di solito, quando ci vengono forniti dati che possiamo visualizzare (dati a 2 o forse anche a 3 dimensioni), l’occhio umano è in grado di formare facilmente cluster distinti. Ma per i pc è un po’ più difficile farlo. È qui che entrano in gioco gli algoritmi di clustering. Essi sono anche molto utili quando dobbiamo gestire dati con un numero di dimensioni maggiori a 3 che nemmeno l’occhio umano è in grado di visualizzare e raggruppare.
Immaginiamo, quindi, di avere 19 punti che hanno questo aspetto:
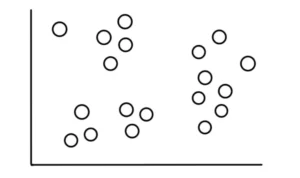
Ora supponiamo di sapere che questi dati rientrano in 3 categorie, relativamente ovvie, che assomigliano a questa:
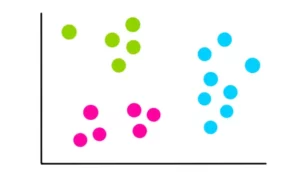
Il nostro compito è quello di utilizzare l’algoritmo K-means per effettuare questa categorizzazione.
Passo 1: Selezionare il numero di cluster k
Il numero di cluster che vogliamo identificare è il parametro k dell’algoritmo. In questo caso, poiché abbiamo ipotizzato che ci siano 3 cluster, k = 3.
Passo 2: Selezionare k punti a caso
Il processo di ricerca dei cluster inizia con la selezione di 3 punti casuali (non necessariamente i nostri punti dati). Questi punti fungeranno da centroidi dei cluster che andremo a creare:
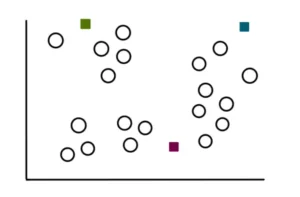
Passo 3: Creare k cluster
Per creare i cluster, iniziamo misurando la distanza di ogni punto da ciascuno dei 3 centroidi. Quindi assegniamo i punti al cluster più vicino. Pertanto, per un punto campione, le distanze appariranno come segue:
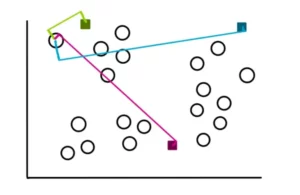
Se osserviamo attentamente, vediamo che la distanza tra il punto e il centroide verde è la minore. Di conseguenza assegniamo il punto al cluster verde.
In due dimensioni, la formula per trovare la distanza tra due punti che di solito viene usata è quella euclidea che è riportata di seguito:
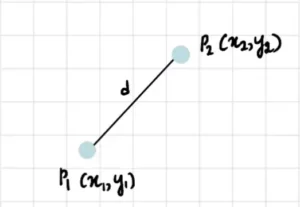
Ovviamente, in alcuni contesti si possono usare altre misure di distanza, come quella di Manhattan, di Minkowski, del coseno o altre. Per comprendere al meglio l’algoritmo useremo quella euclidea.
Utilizzando pertanto la misura euclidea discussa in precedenza, ripetiamo questo processo per il resto dei punti. Alla fine del processo i cluster avranno un aspetto simile a questo:

Passo 4: Calcolo del nuovo centroide di ciascun cluster
Ora che abbiamo ottenuto i nostri 3 cluster, troviamo i nuovi centroidi formati da ciascuno di essi. Ad esempio, il modo in cui calcoliamo le coordinate del centroide del cluster blu è:
dove x1, x2 e x3 sono le coordinate x di ciascuno dei 3 punti del cluster blu. E y1, y2 e y3 sono le coordinate y di ciascuno dei 3 punti del cluster blu. Dividiamo la somma delle coordinate per 3 perché ci sono 3 punti dati nel cluster blu. Allo stesso modo, le coordinate dei centroidi dei cluster rosa e verde sono:
Quindi, i nuovi centroidi saranno:

Passo 5: Valutazione della qualità di ciascun cluster
Poiché k-means non può vedere il clustering come noi, è necessario misurare la qualità del risultato ottenuto trovando la variazione all’interno di tutti i cluster. L’idea di base del k-means consiste nel definire i cluster in modo che la variazione all’interno del cluster sia ridotta al minimo. Per quantificare questa varianza, calcoliamo una cosa chiamata somma dei quadrati all’interno del cluster (WCSS):
dove C sono i centroidi e d i punti in ogni cluster.
Per semplificare, rappresentiamo visivamente la variazione in questo modo:
Passo 6: Ripetere le fasi 3-5
Una volta memorizzati i cluster precedenti e la variazione, si ricomincia da capo. Ma questa volta utilizziamo i centroidi calcolati in precedenza per creare 3 nuovi cluster, ricalcolare il centro dei nuovi cluster e calcolare la somma delle variazioni all’interno di tutti i cluster.
Supponiamo che le successive 4 iterazioni abbiano questo aspetto:
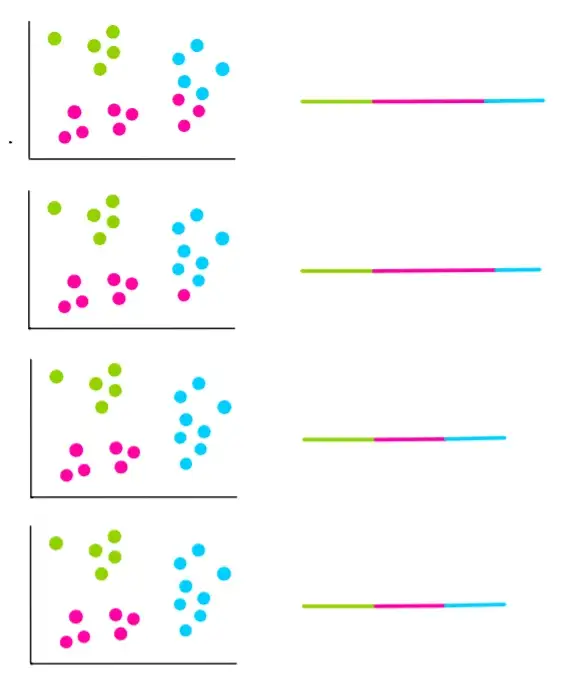
Nelle ultime due iterazioni, possiamo notare che i cluster non sono cambiati. Ciò significa che l’algoritmo è convergente e che il processo di clusterizzazione viene interrotto. Scegliamo quindi i cluster con il WCSS minore, che nel nostro esempio sono quelli delle ultime due iterazioni.
Come si sceglie k?
Nel nostro esempio, sapevamo che avevamo bisogno di 3 cluster. Ma se non sappiamo quanti cluster abbiamo, come facciamo a scegliere k?
In questo caso, proviamo diversi valori di k e calcoliamo il WCSS.
k=1

k=3
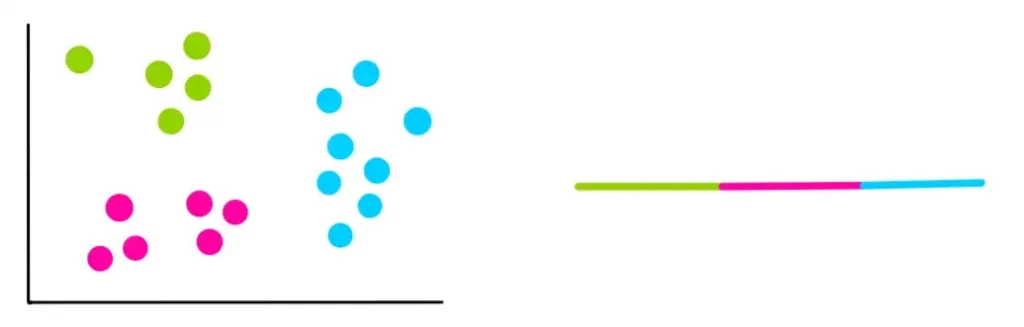
k=2

k=4
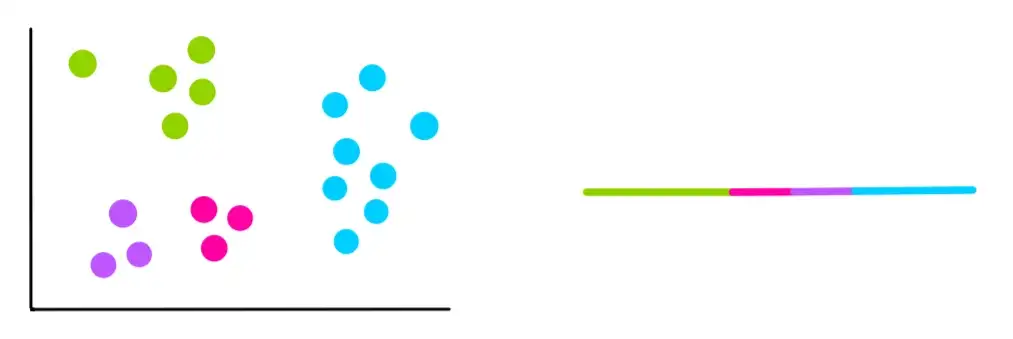
Si può notare che ogni volta che si aggiunge un nuovo cluster, la variazione totale all’interno di ciascun cluster è minore di quella precedente. E quando c’è un solo punto per cluster, la variazione è pari a 0. Quindi, per trovare il miglior k, dobbiamo usare un grafico “a gomito”, che mette in relazione il WCSS con il numero di cluster o k.
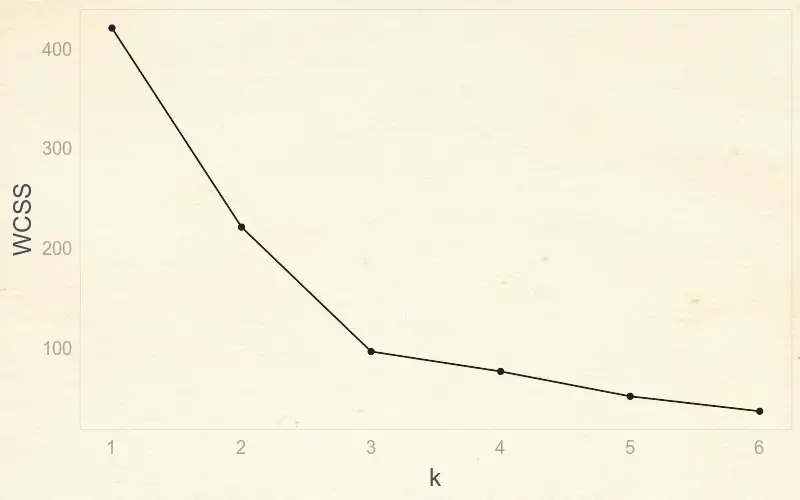
Grazie a questo grafico possiamo trovare il valore ottimale di k semplicemente individuando il “gomito” della curva. Nell’esempio il valore ottimale sarà pari a 3. Infatti, fino a 3 si nota un’enorme riduzione della variazione, mentre dopo questo valore la variazione diminuisce molto più lentamente.
Dove usare il K-Means?
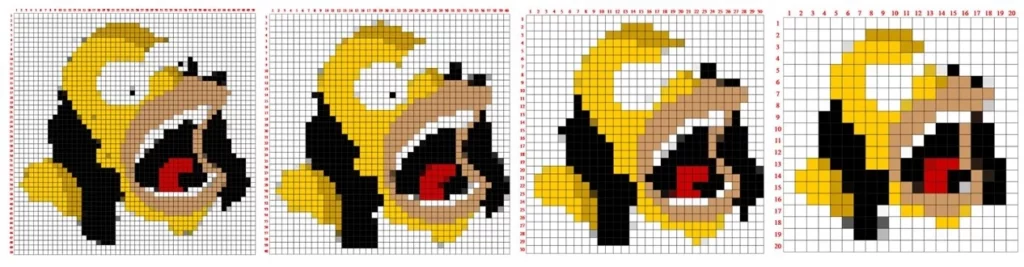
Il k-Means non richiede hardware dedicato e tempi lunghi di processamento dei dati. Pertanto, i campi applicativi sono svariati. Ad esempio, si usa per raggruppare dati GPS per individuare zone “calde” dove avvengono diverse registrazioni. Un’altra applicazione interessante è il processamento delle immagini. Pensate di dover pixelare un’immagine. Usando il K-means, con qualche accortezza, e definendo opportunamente il numero di cluster (griglia) che si vogliono generare si possono le seguenti immagini.
Immagine originale

Immagine pixellata mediante k-means



Una risposta