In molti contesti applicativi, abbiamo la necessità di analizzare i dati per estrarre informazione utile. Ad esempio, potremmo creare dei modelli di classificazione dei clienti di un’assicurazione per assegnare la corretta classe di rischio a nuovi clienti. In altri casi si può essere interessati a raggruppare dati GPS dei veicoli per individuare zone altamente frequentate e/o con traffico elevato. Di algoritmi di analisi dei dai ne esistono una pletora che vanno dai classificatori alle reti neurali, dalle regole di associazione al clustering. In questo articolo affronteremo un algoritmo di clustering chiamato DBSCAN (Density-based spatial clustering of applications with noise).
Come suggerisce il nome, DBSCAN identifica i cluster in base alla densità dei punti. I cluster si trovano solitamente in regioni ad alta densità, mentre gli outlier tendono a trovarsi in regioni a bassa densità. I tre principali vantaggi del suo utilizzo (secondo gli ideatori di questo algoritmo) sono:
- richiede una conoscenza minima del dominio
- può scoprire cluster di forma arbitraria
- è efficiente per database di grandi dimensioni
Di seguito scopriremo come funziona passo passo.
Algoritmo
Supponiamo che i nostri dati grezzi abbiano questo aspetto:
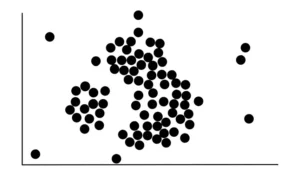
La prima cosa da fare è contare il numero di punti vicini a ciascun punto. La vicinanza si determina disegnando un cerchio di un certo raggio (eps) attorno a un punto e ogni altro punto che cade in questo cerchio si dice che è vicino al primo punto. Ad esempio, iniziamo con questo punto rosso e tracciamo un cerchio intorno ad esso.
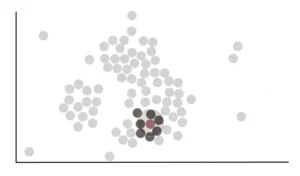
Vediamo che il cerchio tracciato per questo punto include, completamente o parzialmente, ad altri 7 punti. Quindi possiamo dire che il punto rosso è vicino a 7 punti.
Il raggio del cerchio, chiamato eps, è il primo parametro dell’algoritmo DSBCAN che dobbiamo definire. La scelta del valore di eps è cruciale. Infatti, se scegliamo un valore troppo piccolo, gran parte dei dati non verrà raggruppata. D’altra parte, se si sceglie un valore troppo grande, i cluster si fonderanno e molti punti dei nostri dati si troveranno nello stesso cluster. In generale, è preferibile un valore di eps più piccolo.
Consideriamo ora questo punto verde. Vediamo che è vicino a 3 punti perché il suo cerchio con raggio eps si sovrappone ad altri 3 punti.
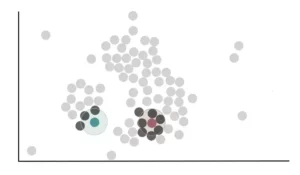
Allo stesso modo procediamo per tutti i punti rimanenti, contando il numero di punti vicini. Una volta fatto questo, dobbiamo decidere quali punti sono i core points e quali non lo sono.
È qui che entra in gioco il secondo parametro dell’algoritmo: minPoints. Utilizziamo minPoints per determinare se un punto è un core point o meno. Se impostiamo minPoints a 4, diciamo che un punto è un core point se almeno 4 punti sono vicini ad esso. Se il numero dei vicini di un punto è inferiore a 4, questo viene considerato un non core point.
Come regola generale, minPoints ≥ numero di dimensioni in un dataset + 1. Valori più grandi sono generalmente migliori per i dataset con rumore. Il valore minimo di minPoints deve essere 3, ma più grande è il nostro dataset, più grande deve essere il valore di minPoints.
Per il nostro esempio, impostiamo il valore di minPoints a 4. In questo modo possiamo dire che il punto rosso è un Core Point perché almeno 4 punti sono vicini ad esso, mentre il punto blu è un Non-Core Point perché solo 3 punti sono vicini ad esso.
In definitiva, utilizzando il processo sopra descritto, possiamo determinare che i seguenti punti evidenziati sono Core point.
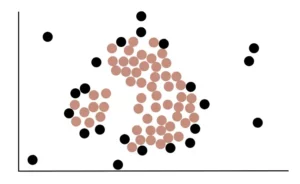
I punti neri, invece, sono punti Non-Core Point.
Ora scegliamo a caso un punto centrale e lo assegniamo al primo cluster. Qui, selezioniamo a caso un punto e lo assegniamo al cluster verde.
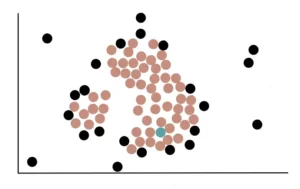
I Core point che sono vicini al cluster verde, cioè che si sovrappongono al cerchio con raggio eps verranno aggiunti al cluster verde.
Pertanto, i core point vicini al cluster verde che man mano sta crescendo vengono aggiunti ad esso. Nell’esempio riportato di seguito, possiamo notare che 2 core point e 1 punto Non-Core Point sono vicini al cluster verde. Solamente i 2 core point saranno aggiunti al cluster.
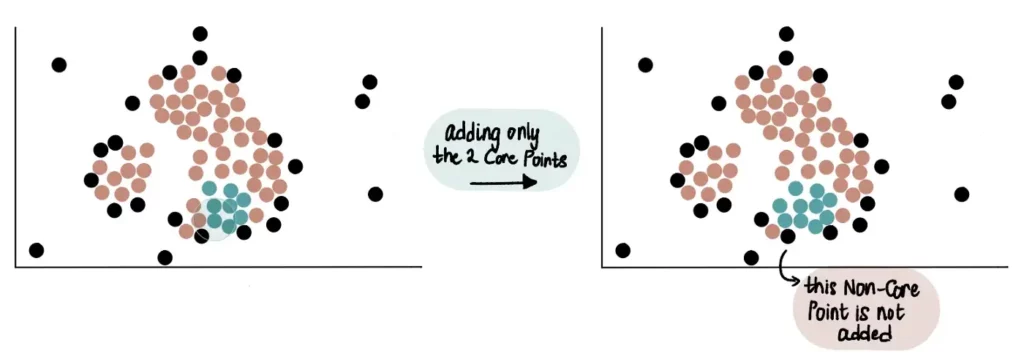
Alla fine, tutti i core point che sono vicini al cluster verde saranno aggiunti ad esso e i dati appariranno così:
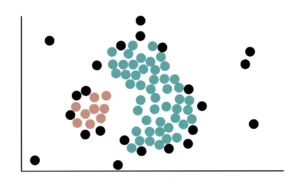
Infine, si aggiungono tutti i Non-Core Point vicini al cluster verde. Ad esempio, questi 2 Non-Core Point sono vicini al cluster blu, pertanto vengono aggiunti:
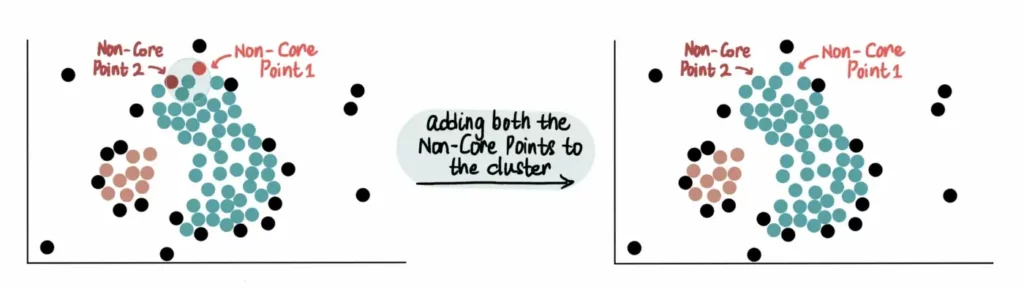
Tuttavia, poiché non sono core point, non li utilizziamo per estendere ulteriormente il cluster blu. Ciò significa che l’altro Non-Core Point vicino al punto Non-Core 1 non verrà aggiunto al cluster verde.
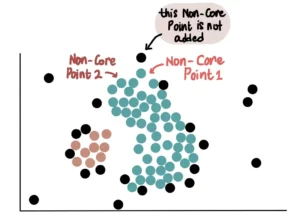
Quindi, a differenza dei core point, i Non-Core Point possono solo unirsi ad un cluster ma non possono essere usati per estenderlo ulteriormente.
Dopo aver aggiunto tutti i Non-Core Point, abbiamo creato il nostro cluster blu, che si presenta così:
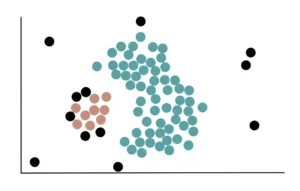
Poiché nessuno dei core point rimanenti è vicino al primo cluster, iniziamo il processo di formazione di un nuovo cluster. Innanzitutto, scegliamo a caso un punto centrale (che non si trova in un cluster) e lo assegniamo al nostro secondo cluster giallo.
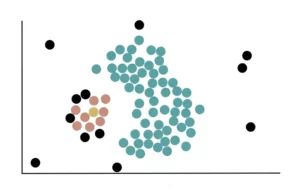
Aggiungiamo, quindi, tutti i core point vicini al cluster giallo e li usiamo per estendere ulteriormente il cluster.
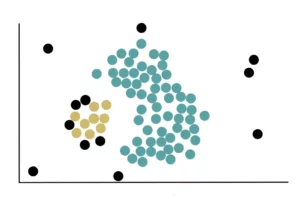
Infine, vengono aggiunti i Non-Core Point che si trovano vicino al cluster giallo. Dopo aver fatto questo, i nostri dati con i 2 cluster appaiono così:

Continuiamo a ripetere questo processo di creazione di cluster fino a quando non ci sono più core point. Nel nostro caso, poiché tutti i punti centrali sono stati assegnati ad un cluster, abbiamo finito di creare nuovi cluster. I Non-Core Point rimasti che non sono vicini ai core point e non fanno parte di alcun cluster sono chiamati outlier.
In questo modo, abbiamo creato i nostri 2 cluster e trovato pure gli outlier.
DBSCAN vs K-Means vs clustering gerarchico
Esistono anche altri tipi di algoritmi di clustering. Quelli più popolari sono il K-means e il clustering gerarchico che analizzeremo in altri articoli. Questi due algoritmi sono impiegati per identificare cluster compatti, ben separati e di forma globulare. Soffrono, però, la presenza di rumore e di valori anomali nei dati. D’altra parte, DBSCAN cattura cluster di forma complessa e fa un ottimo lavoro nell’identificare gli outlier. Un altro aspetto positivo di DBSCAN è che, a differenza di K-Means, non è necessario specificare il numero di cluster (k): l’algoritmo li trova automaticamente. La figura seguente riporta alcuni esempi di dataset e i differenti risultati ottenuti mediante il DBSCAN e il k-means. Si può evincere che in alcuni contesti (cluster globulari e ben separati) i due algoritmi ottengono risultati analoghi, mentre in altri casi è opportuno scegliere l’algoritmo che mostra un comportamento più solido rispetto alla distribuzione dei dati.




Una risposta